by Rajarshee Das (a L.E.A.P. writer)

[PART OF HARTS’S 2020 XMAS SPECIAL]

Hello Everyone, this is Rajarshee. Today I’m here with one of the most beautiful, no the most beautiful thing known to me, yes I’m talking about Euler’s circle, Feuerbach Circle, Nine Point circle or whatever you call it. I think it’s the most beautiful circle known to mankind! Today we will understand it from scratch. (This is an informative article, so I’ll not go with the proofs. This will also make the article look clumsy. Also try to do the constructions along with me; this would give a better understanding of the concept. You may take help from GeoGebra or a geometry box).

Let us start with triangle ABC.

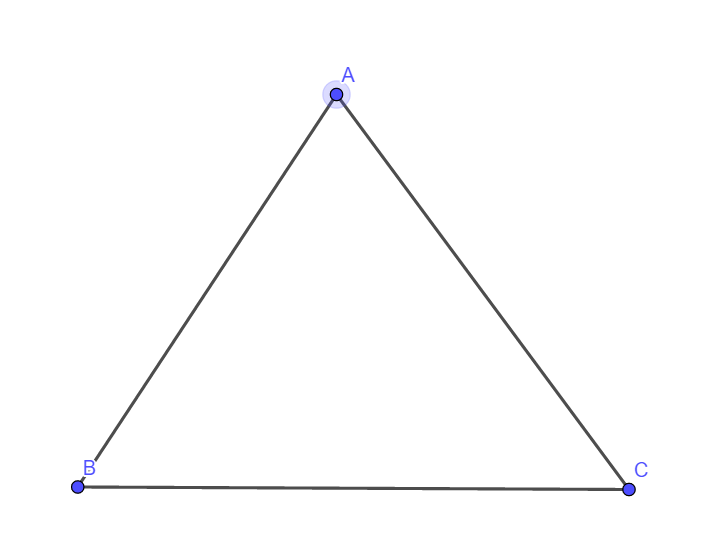
Now let’s draw the altitudes from A, B & C.

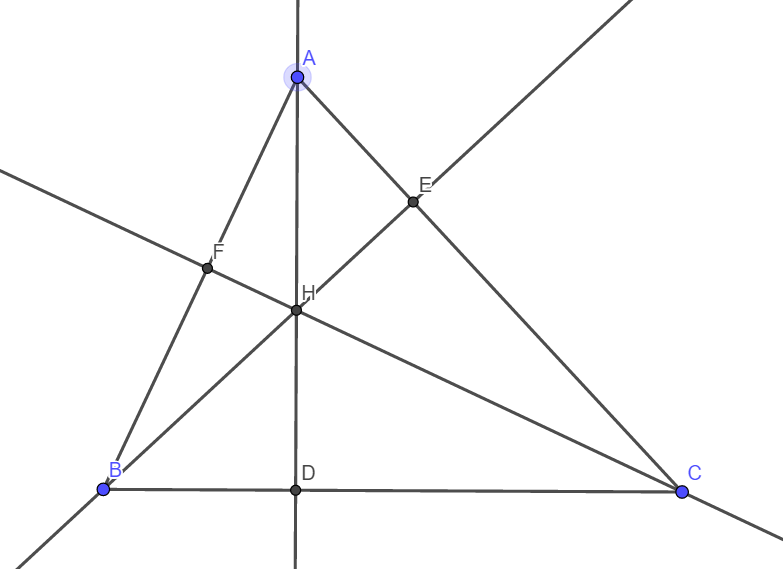
Here AD, BE and CF are the altitudes from A, B and C to sides BC, AC and AB respectively. Note the point where all the altitudes meet. This is a very special point of a triangle and is known as Orthocenter and it is denoted by H. Now join DE, EF and FD.

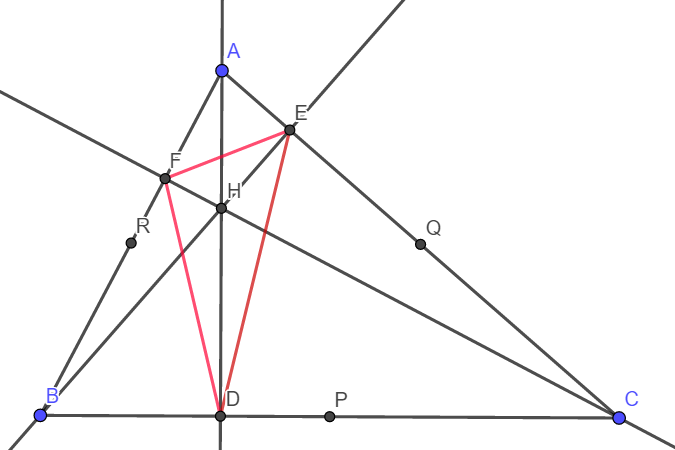
This triangle DEF is known as Pedal triangle of triangle ABC. We will talk about it some other day. But today what we will talk about is the circumcircle of this pedal triangle I.e., triangle DEF. Note that P,Q and R are the midpoints of side BC, CA and AB.

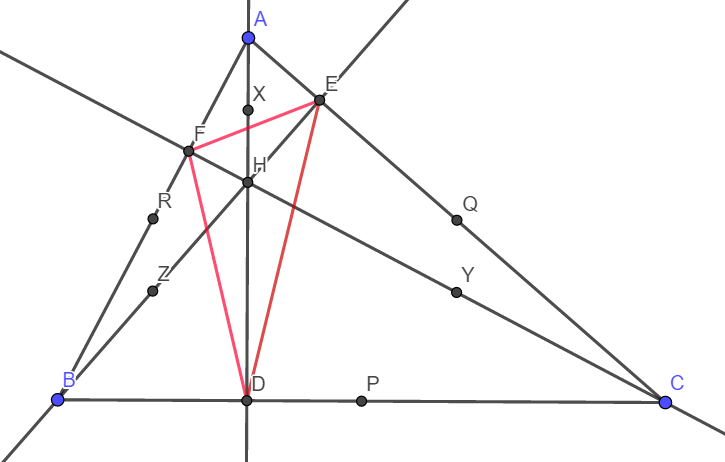
X, Y and Z are the midpoints of the line joining AH,CH and BH.

Now let’s construct the circumcircle of triangle DEF and see what we get.

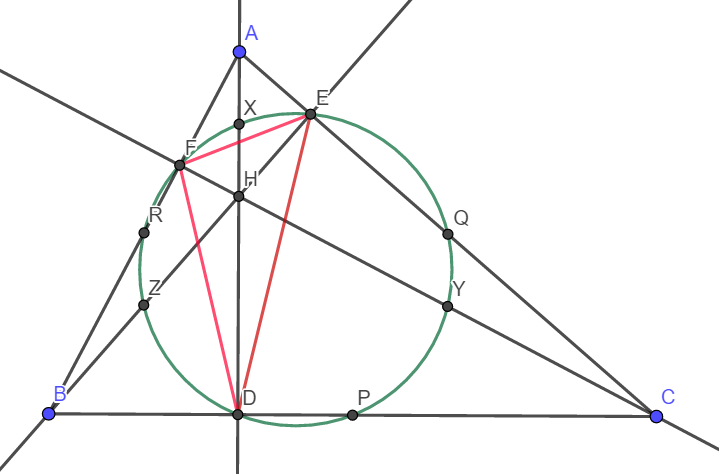
What is this!!! The circumcircle of triangle DEF is also passing through X,Y,Z,P,Q and R !!! Amazing, isn’t it? This circle is called “Nine point circle” as it passes through 9 significant concyclic points:
• Three feet of altitudes from vertices of triangle ABC
• Three midpoints of the sides of triangle ABC and
• Three midpoints of AH, BH, and CH where H is the orthocenter of the triangle.
This is true for any kind of triangle (except Right angled triangles). These nine points would always lie together in a same circle.
Another interesting fact about nine point circle is that THE MIDPOINT OF THE LINE JOINING CIRCUMCENTER AND ORTHOCENTER OF A TRIANGLE IS THE CENTRE OF NINE-POINT CIRCLE. IT’S CENTER IS KNOWN AS NINE POINT CENTER OF A TRIANGLE.
Nine point circle was first described by KARL WILHELM FEUERBACH that is why it is also known as Feuerbach’s Circle.
But Feuerbach didn’t describe all the nine points at once. He described the six -point circle recognizing the significance of midpoints of the three sides of the triangle ABC and feet of altitudes of triangle ABC. That is why this circle is sometimes referred to as SIX-POINT CRICLE. But soon later mathematician OLRY TERQUEM found that the midpoints of AH, BH and CH I.e., X, Y and Z also lie on the circle.

That is why Nine-Point circle is also called TERQUEM’S CIRCLE.
In 1822 Feuerbach discovered that nine-point circle of any triangle is externally tangential to the three excircles and internally tangential to the incircle of the triangle. This result is known as Feuerbach’s Theorem. The point at which the incircle and Nine- Point circle touch each other is known as Feuerbach point.

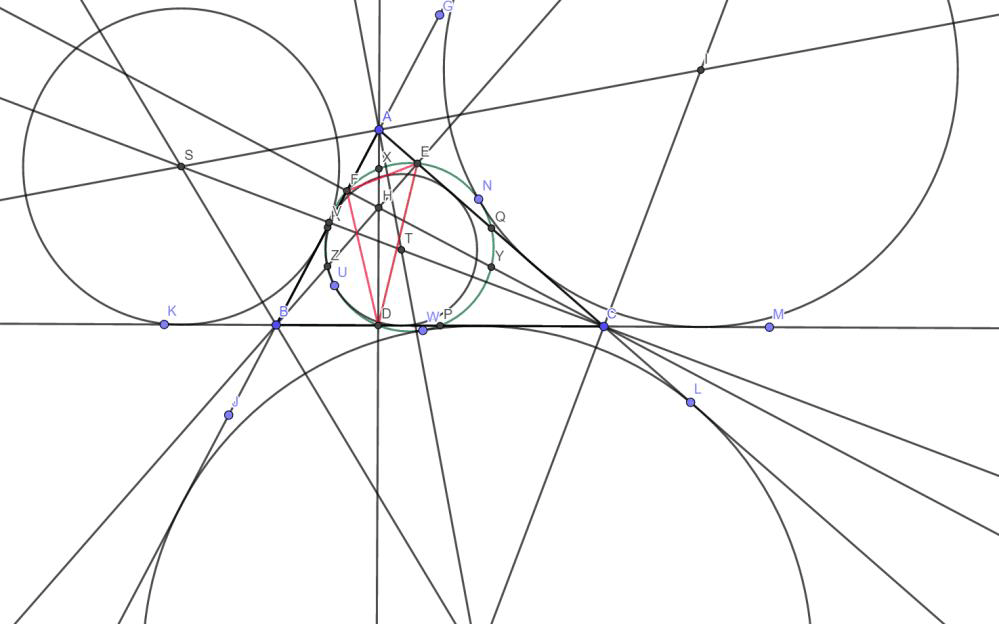
This is what we have done till now. The green circle is our nine point circle. Look it is tangential to the 3 excircles and the incircle.
Another important property of Nine-Point Circle is that the radius of nine point circle is half the circumradius of triangle ABC. One thing to be noted about nine point center is that it lies on the famous Euler’s line in a triangle. That is why sometimes it is also referred to as Euler’s circle.

So this was all for today. Hope you like my content.

And thanks to GeoGebra for helping me doing these constructions.

Seeing You all soon in next article. Bye!